Final Review
Nama : Raymond Andilsim
NIM : 2301906533
Final Review Semester 2 :

BST memiliki aturan seperti :
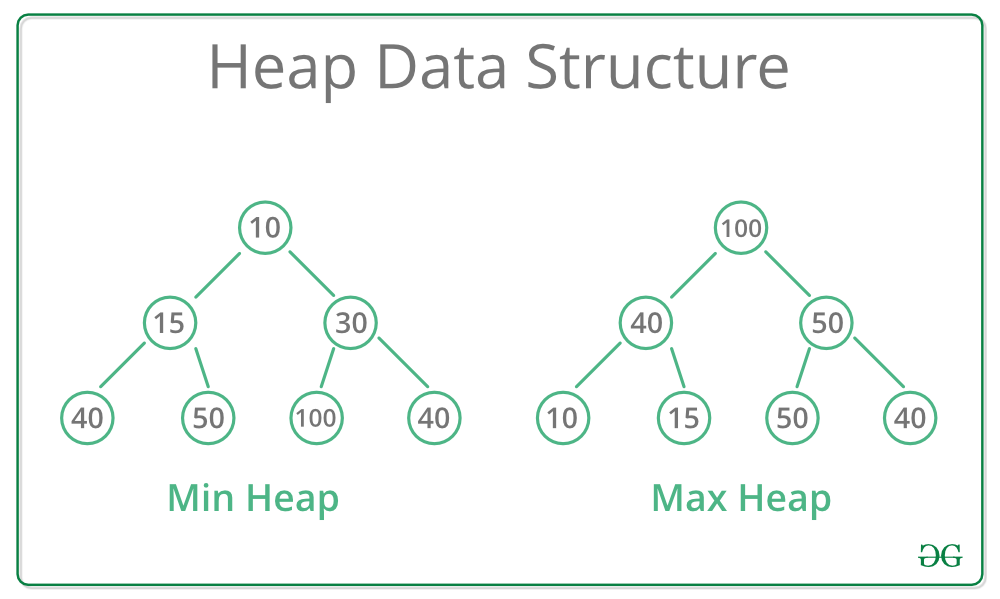
Max-Heap: Dalam Max-Heap kunci yang ada di simpul akar harus paling besar di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub-pohon di Pohon Biner itu.
Min-Heap: Dalam Min-Heap kunci yang ada di simpul akar harus minimum di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub- pohon di Pohon Biner itu.
NIM : 2301906533
Nama Dosen:
(Kelas Besar) : Ferdinand Ariandy Luwinda (D4522) & Henry Chong (D4460)
(Kelas Kecil) : Alexander (D5319)
Final Review Semester 2 :
Linked List
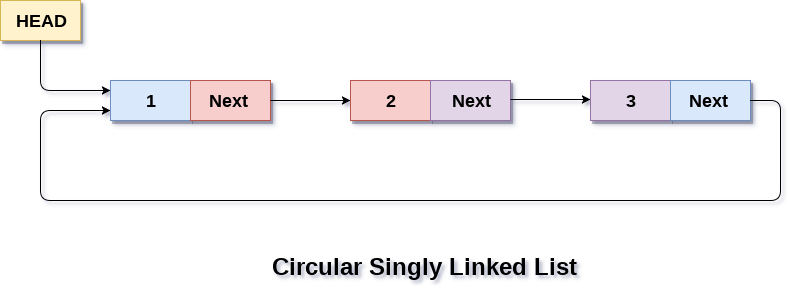
1. Circular Single Linked List
Circular linked list adalah variasi dari linked list dimana setiap node tidak memiliki ruang NULL dan diganti oleh ruang untuk menunjuk node selanjutnya dan node paling terakhir akan menunjuk node yang pertama dan seterusnya, sehingga terbentuk sebuah siklus.
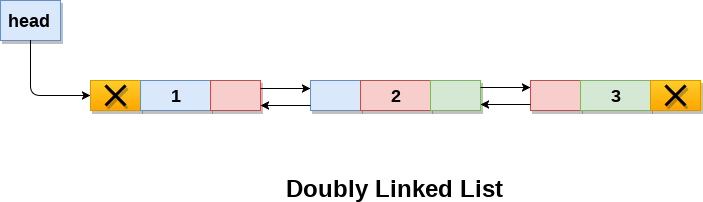
2. Double Linked List
Double Linked List adalah variasi dari linked list yang bisa bergerak bolak-balik dimana setiap node memiliki 3 ruang, perbedaan node pertama, node tengah dan node terakhir adalah di node pertama, di ruang pertama adalah NULL dan ruang ketiga untuk menunjuk node selanjutnya, untuk node di tengah, ruang pertama untuk menunjuk node sebelumnya dan ruang ketiga untuk menunjuk node selanjutnya, dan di node terakhir, ruang pertama untuk menunjuk node sebelumnya dan ruang ketiga adalah NULL.
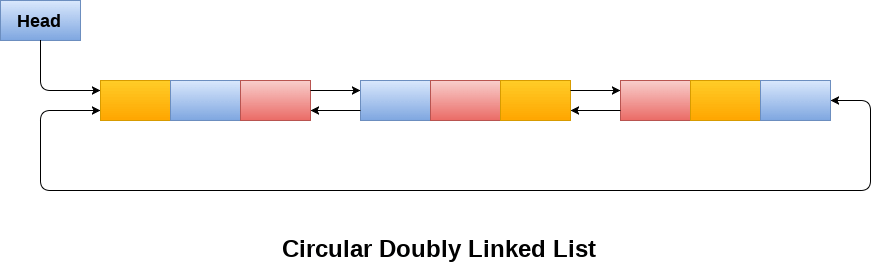
3. Circular Doubly Linked List
Circular Doubly Linked List adalah linked list gabungan dari circular single linked list dan double linked list, dimana setiap node bisa menunjuk node selanjutnya maupun sebelumnya dan node terakhir akan menunjuk node pertama, dan akan membentuk sebuah siklus.
Push dan Pop di Single Linked List
Push
void push(int a)
{
curr = (struct Data*)malloc(sizeof(struct Data));
curr->value = a;
if(head==NULL){
head = tail = curr;
}
else{
curr->next = head;
head = curr;
}
}
Pop
void pop()
{
curr = head;
if(curr == tail){
free(curr);
head = tail = NULL;
}
else if(curr != NULL)
{
head = head->next;
free(curr);
}
Push dan Pop di Double Linked List
Push
void push(int a)
{
curr = (struct Data*)malloc(sizeof(struct Data));
curr->value = a;
if(head==NULL){
head = tail = curr;
}
else{
tail->next = curr;
curr->prev = tail;
tail = curr;
}
head->prev = tail->next = NULL;
}
Pop
void pop()
{
curr = head;
if(tail == head){
free(curr);
tail = head = curr = NULL;
}
else
{
while(curr->next!=tail){
curr = curr->next;
}
free(tail);
tail = curr;
tail->next = NULL;
}
}
Hashing Table and Binary Tree
Hashing Table
Hash Table adalah struktur data yang menyimpan data secara asosiatif. Dalam tabel hash, data disimpan dalam format array, di mana setiap nilai data memiliki nilai indeks uniknya sendiri. Akses data menjadi sangat cepat jika kita mengetahui indeks dari data yang diinginkan.
Dengan demikian, itu menjadi struktur data di mana operasi penyisipan dan pencarian sangat cepat terlepas dari ukuran data. Tabel hash menggunakan array sebagai media penyimpanan dan menggunakan teknik hash untuk menghasilkan indeks di mana elemen yang akan dimasukkan atau harus ditempatkan dari.

Hubungan Hashtable dan Blockchain
- Hash adalah fungsi yang memenuhi tuntutan terenkripsi yang diperlukan untuk menyelesaikan perhitungan blockchain
- Hash seperti solusi atau tulang punggung jaringan blockchain
- Hash memiliki panjang yang tetap dan hampir tidak mungkin untuk ditebak panjangnya jika seseorang mencoba untuk memecahkan atau mencoba masuk ke blockchain
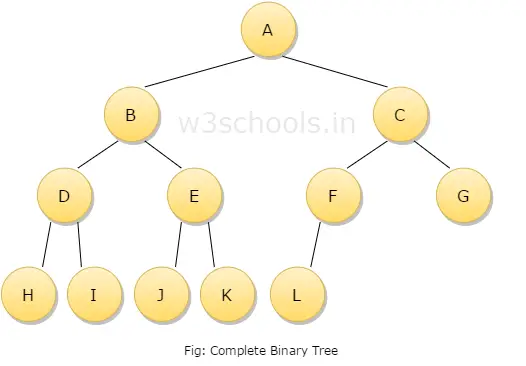
Binary Tree
Binary tree adalah pohon khusus dimana disetiap node atau vertex bisa tidak memiliki cabang atau juga bisa memiliki 1 atau 2 cabang dan setiap cabang bisa bercabang lagi dan memiliki sifat yang sama. Binary tree digunakan untuk mewakili struktur data nonlinear. Pohon biner memiliki peran penting dalam software application dan salah satu hal paling penting dari Binary Tree adalah searching dalam algoritma.

AVL Tree
AVL Tree adalah subtipe dari Binary Search Tree. Pohon AVL memiliki properti penyeimbangan mandiri dinamis selain semua properti yang digunakan oleh Binary Search Tree. AVL Tree adalah sebuah upgrade dari Binary Search Tree. Tambahan/Upgraden dari BST adalah :
BST memiliki aturan seperti :
- Setiap pohon memiliki root (di atas).
- Root memiliki nol, satu atau dua node anak.
- Setiap node memiliki nol, satu atau dua node anak, dan seterusnya.
- Setiap node memiliki hingga dua anak.
- Untuk setiap node, turunan/node kirinya lebih kecil dari node di atasnya, yang lebih kecil dari turunan kanan.
- Jika ada ketidakseimbangan pada anak kiri subtree kanan, maka kita akan melakukan rotasi kiri-kanan.
- Jika ada ketidakseimbangan pada anak kiri subtree kiri, maka kita akan melakukan rotasi kanan.
- Jika ada ketidakseimbangan pada anak kanan subtree kanan, maka kita akan melakukan rotasi kiri.
- Jika ada ketidakseimbangan pada anak kanan subtree kiri, maka kita akan melakukan rotasi kanan-kiri.
Contoh Single Rotation
 |
| Node 37 dan 40 tidak seimbang karena terdapat 45 di paling bawah kanan dan beda nodenya itu sudah 2, maka itu di rotate menjadi : |
Contoh Double Rotation
 |
Terjadi tidak keseimbangan karena ada 5 di paling bawah sebelah kiri dan sudah terjadi perbedaan 2 node, sehingga dilakukan rotasi pertama di 11 : |
 |
11 sudah terotasi dan 8 naik ke atas, tetapi masih belum seimbang, maka itu dilakukan lagi rotasi kedua di 3 dan 8 bisa naik lagi ke node atas : |
 |
Tree sudah seimbang karena perbedaan nodneya sekarang hanya 1. |
Heap and Tries
Heap
Heap adalah struktur data berbasis pohon khusus di mana pohon itu adalah pohon biner lengkap. Secara umum, tumpukan dapat terdiri dari dua jenis:Max-Heap: Dalam Max-Heap kunci yang ada di simpul akar harus paling besar di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub-pohon di Pohon Biner itu.
Min-Heap: Dalam Min-Heap kunci yang ada di simpul akar harus minimum di antara kunci yang ada di semua anak-anak itu. Properti yang sama harus benar secara rekursif untuk semua sub- pohon di Pohon Biner itu.

Insertion
Suppose the Heap is a Max-Heap as:
10
/ \
5 3
/ \
2 4
The new element to be inserted is 15.
Process:
Step 1: Insert the new element at the end.
10
/ \
5 3
/ \ /
2 4 15
Step 2: Heapify the new element following bottom-up
approach.
-> 15 is more than its parent 3, swap them.
10
/ \
5 15
/ \ /
2 4 3
-> 15 is again more than its parent 10, swap them.
15
/ \
5 10
/ \ /
2 4 3
Therefore, the final heap after insertion is:
15
/ \
5 10
/ \ /
2 4 3
Deletion
Suppose the Heap is a Max-Heap as:
10
/ \
5 3
/ \
2 4
The element to be deleted is root, i.e. 10.
Process:
The last element is 4.
Step 1: Replace the last element with root, and delete it.
4
/ \
5 3
/
2
Step 2: Heapify root.
Final Heap:
5
/ \
4 3
/
2
Trie
Tries adalah struktur data yang sangat spesial dan berguna yang didasarkan pada awalan string. Mereka digunakan untuk mewakili "Pengambilan" data dan dengan demikian nama Trie.
Prefix: prefix adalah awalan string tidak lain adalah huruf apa saja yang dapat dianggap dimulai dari awal string. Misalnya, kata "abacaba" memiliki awalan berikut:
ab
aba
abac
abaca
abacab
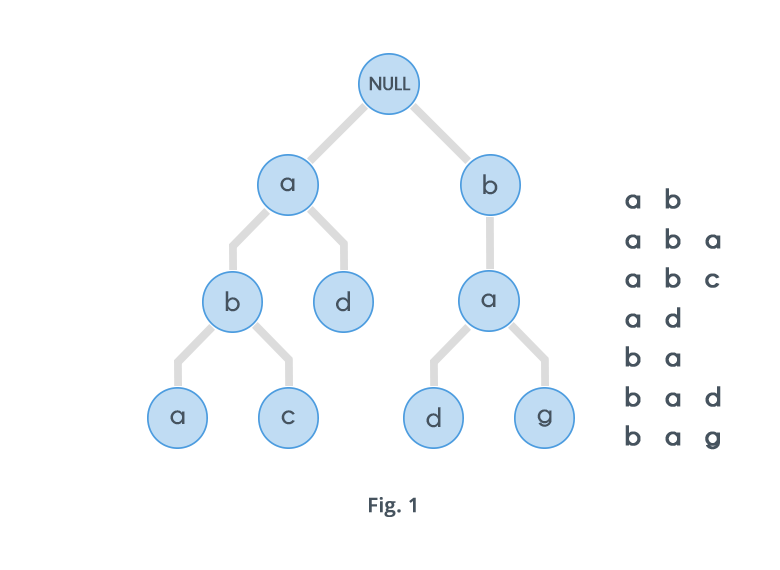
Trie adalah struktur data khusus yang digunakan untuk menyimpan string yang dapat divisualisasikan seperti grafik. Terdiri dari node dan edge. Setiap simpul terdiri dari maksimal 26 anak dan ujung-ujungnya menghubungkan setiap simpul induk ke anak-anaknya. 26 pointer ini tidak lain adalah pointer untuk masing-masing 26 huruf alfabet Inggris. Tepi terpisah dipertahankan untuk setiap tepi.
String disimpan dengan cara top to bottom berdasarkan awalan mereka dalam sebuah trie. Semua awalan panjang 1 disimpan sampai level 1, semua awalan panjang 2 diurutkan sampai level 2 dan seterusnya.
Misalnya, perhatikan diagram berikut:
Prefix: prefix adalah awalan string tidak lain adalah huruf apa saja yang dapat dianggap dimulai dari awal string. Misalnya, kata "abacaba" memiliki awalan berikut:
ab
aba
abac
abaca
abacab
Trie adalah struktur data khusus yang digunakan untuk menyimpan string yang dapat divisualisasikan seperti grafik. Terdiri dari node dan edge. Setiap simpul terdiri dari maksimal 26 anak dan ujung-ujungnya menghubungkan setiap simpul induk ke anak-anaknya. 26 pointer ini tidak lain adalah pointer untuk masing-masing 26 huruf alfabet Inggris. Tepi terpisah dipertahankan untuk setiap tepi.
String disimpan dengan cara top to bottom berdasarkan awalan mereka dalam sebuah trie. Semua awalan panjang 1 disimpan sampai level 1, semua awalan panjang 2 diurutkan sampai level 2 dan seterusnya.
Misalnya, perhatikan diagram berikut:


Comments
Post a Comment